文章节选于csapp 3rd edition.

整数表示

无符号整数表示

无符号整数是最简单的。由每一位二进制的0/1和二次幂累加而成。

\[ X=\sum_{i=0}x_i 2^i \]

二进制串0001映射到\(0 \times 2^3 + \cdots + 1 \times 2^0 = 1\). 容易推出，uint32的最大值是\(2^32 -1\).

有符号整数表示

现代计算机基本采用补码表示，反码和原码已经近乎退出历史舞台了。补码的最高有效位是1时，它的权重是\(-2^{w-1}\). 容易推出，0xFF等于-1，而0x7F是8位有符号的最大数127,0x80是8位有符号的最小数-128。补码在0处和正溢出的时候都有比较良好的性质，可以仅靠加法就可实现从-1(0xFF)到0(0x00)的进位。

补码的Tmin等于-Tmax-1,所以其区间是不对称的。取相反数、绝对值的时候要注意处理边界情况。补码的相反数等于所有位取反再+1，所以0x80取反的结果是0x7F,加一后会回到0x80,这暗示了对Tmin取反会回到Tmin，因为发生了溢出。

扩展和截断数字的位表示

扩展数字

无符号数字的扩展直接在前面填0，例如从8位数字到16位无符号，0xFF => 0x00FF. 有符号数字需要执行符号扩展，一个颇有启发的例子是从有符号的8位数字到16位数字，-1(0xFF) => -1(0xFFFF)。这暗示了如果有符号数字进行扩展，需要复制最高位的位。

截断数字

无符号的数字在前面直接截断，(65535)0xFFFF截断到8位等于(255)0xFF,而有符号的数字截断中可能会出现符号改变，比如(32367)0x7fff截断后(-128)0xff。

浮点数表示

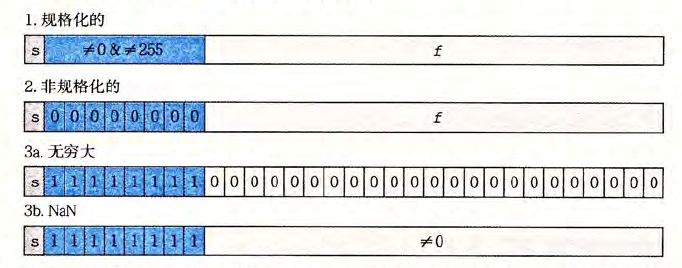
浮点数被编码成\(-1^s \times M \times 2^E\),其中s是第一位二进制，代表这是正数or负数，exp段代表了阶码E，而后面的frac段编码尾数M。在float下，s,exp,frac分别由1,8,23位。浮点数编码有三种模式，分别为规格化的值，非规格化的值和特殊值。

规格化： exp不全为0也不全1，此时阶码E的值为e - Bias，e为exp段编码的无符号数，Bias为\(2^{k-1} - 1 \),而尾数段M为1 + m,其中m为尾数段编码的小数，\(\frac{1}{2} + \frac{1}{4} + \cdots \)，这种古怪的编码格式提供了从非规格化到规格化的平滑过渡。

非规格化： exp全为0，此时M的值不再加1，只编码小数，而E的值为1 - Bias，这样当0x0000和0x8000出现的时候，可以得到+0.0和-0.0.

特殊值 exp全是1，这样frac段全0的时候代表无穷和负无穷，frac不为0时候代表nan。

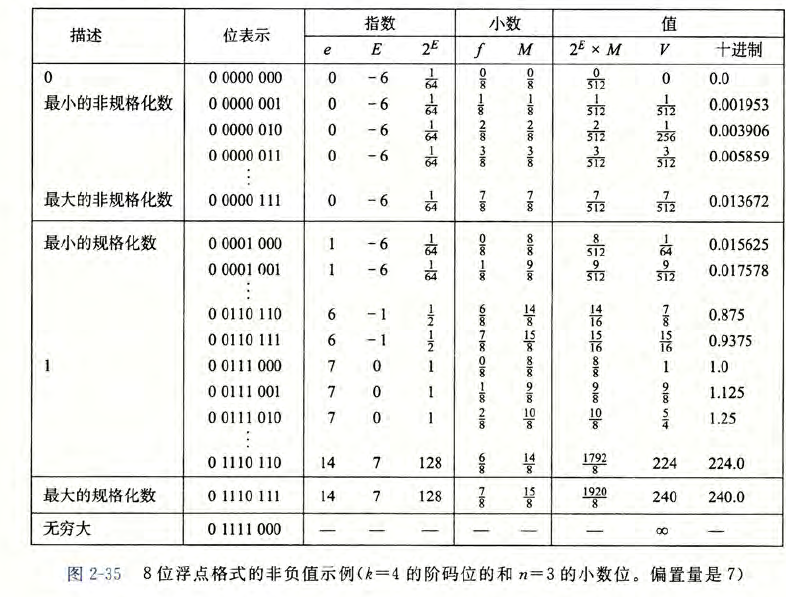
一个8位浮点格式的例子（1位符号，4个阶码和3个frac段），可以编码的最大非无穷值为(0x0 1110 111) = \(1 \times 2 ^ {14 - 7} \times (1 + \frac{7}{8}) = 240\)

Reference

• csapp