渲染方程的可解性
先上渲染方程
\[ \textcolor{red}{L_r(p,\omega_r)} = \textcolor{blue}{L_e(p,\omega_o)} + \int_{\Omega^+} \textcolor{blue}{f_r(\omega_i \Rarr \omega_r )}\textcolor{red}{ L_i(p,\omega)} \textcolor{blue}{\cos\theta_i \text{d}\omega_i}\\ where: \cos\theta_i = \mathbf{n} \cdot \mathbf{w_i} \]
方程中蓝色的量代表已知量,红色代表未知量。 左边和右边的\(\mathbf{L}\)项都是未知的,其他项都是已知的。
根据Linear Operator Theory,可以整理为一个线性系统的方程
\[ \textcolor{red}L = \textcolor{blue}E + \textcolor{blue}K\textcolor{red}L \]
简单的理解可以理解为\(L\)代表一个列向量,包含了场景中所有的光源,\(E\)代表材质的自发光项,而\(K\)代表一个矩阵,代表光线弹射中的变换,比如BRDF。 根据解线性方程的一般方法,我们移动方程左右项得到解
\[ \textcolor{red}{L} = \textcolor{blue}{ (I - K) ^{-1}E} \]
根据泰勒展开,普通函数\(\frac{1}{1 - x}\)的展开式为\( 1 + x + x^2 + \cdots\),对向量\( \mathbf{( I - K)} ^ {-1}\)做泰勒展开可以得到
\[ \textcolor{red}{L} = \textcolor{blue}{( I + K + K^2 + K^3 + \cdots)E} \]
由此解得:
- 一阶泰勒展开的时候,\( L = E\), 场景只有光源可见
- 二阶泰勒展开的时候,\( L = E + KE\), 场景只有光源和一次对光源的变换,代表是
Blinn-Phong光照模型 - 三阶泰勒展开的时候,\( L = E + KE + K^2 E\), 场景有光源和一次对光源的变换以及一次光线间接弹射,此时已经能模拟镜面材质,但是无法处理透明折射类材质,因为折射类材质至少需要 从光源到表面->折射光线内部折射->折射光线从内部射出两次间接弹射。
- 由于\(\mathbf{K}\)的行列式必定不可能大于一(根据BSDF的性质以及能量守恒),所以光线间接弹射的越多,\(K^n\)逐渐趋向于0,贡献越少。
来自CS348B的示例
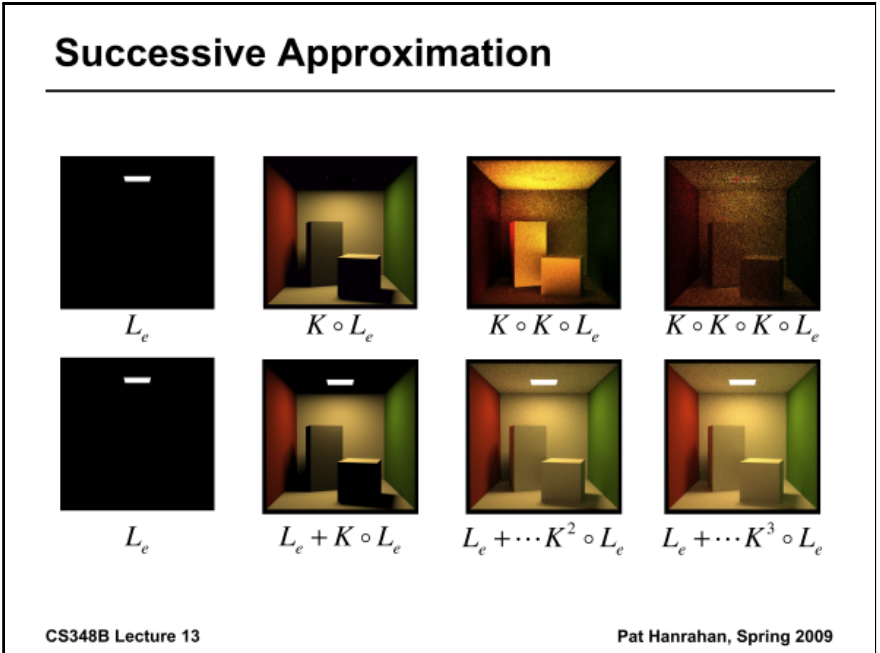
蒙特卡罗积分
这里直接给出蒙特卡罗积分的计算方法。
给定函数\(f(x)\)服从概率密度\(p(x)\)的随机分布,则
\[ \int_a^b{f(x)}dx = \int_a^b{\frac{f(x)}{p(x)}p(x)}dx = E(\frac{f(x)}{p(x)}) \approx \frac{1}{N} \sum_{i = 1}^N{\frac{F(X_i)}{p(X_i)}} \]
由此套入渲染方程中展开
\[ \int_{\Omega^+} f_r(\omega_i \Rarr \omega_r )L_i(p,\omega_i)cos\theta_i \text{d}\omega_i \approx \frac{1}{N}\sum_{i = 1}^N{\frac{f_r(\omega_i \Rarr \omega_r )L_i(p,\omega_i)cos\theta_i}{pdf(w_i)}} \]
对这个方程中我们知道除了\(L_i\)以外的所有量,而\(L_i\)的值可以靠递归求解的方式算出来,将\(L_i\)的值当作下一次光线弹射得到的\(L_o\)值,直到递归达到最大深度(返回0值)或者到达递归停止条件(光线到达光源)。
重要性采样
考虑如下图片中的函数,对该函数进行均匀采样,蓝色代表函数图像的分布,绿色代表采样点的概率分布。
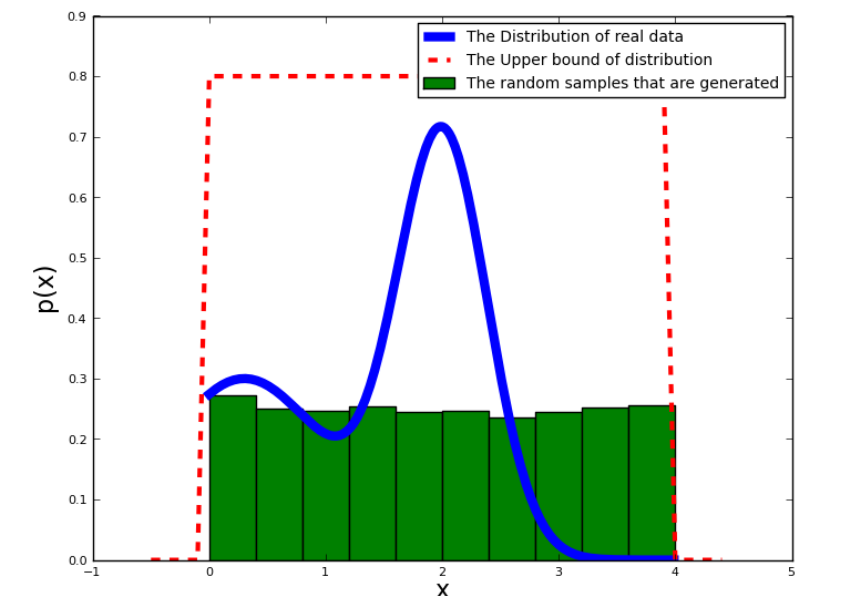
可以见到大约四分之一的采样点都浪费了,因为蓝色函数对大于3的部分几乎为0,而中间特别显著的部分采样不足。在蒙特卡洛积分中,\(\frac{1}{N} \sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}\)中的\(f(x)\) 和 \(p(x)\)应该尽可能的相似。但是很遗憾,\(f(x)\)是未知的。因为蒙特卡罗积分的目的是求\(\int_0^{\infin}{f(x)}\),如果已知\(f\)的形状那么可以直接获得解析解。
一个简单的渲染中的重要性采样是cosine采样,因为diffuse材质的brdf为常数
\[ f_r(\omega_i \Rarr \omega_r ) = \frac{\vec{k_a}}{\pi} \]
由此可以写出渲染方程中未知部分的方程为
\[ \frac{1}{N}\sum_{i = 1}^N\frac{k_a / \pi L_i(p,\omega_i)cos\theta_i}{pdf(w_i)} \]
观察分子,我们可以发现分子的部分至少可能和\(\cos(\theta_i)\)形状接近,由此我们可以令\(pdf\)函数的形状正比于\(\cos(\theta_i)\) 根据pdf积分为1的性质,我们可以推导出
\[ \int_{\Omega^+} p(x) d\omega = 1\\ p(x) = \frac{\cos(\theta_i)}{\pi} \]
这就是最简单的重要性采样: cosine采样。 具体过程可见PBRT3
Reference:
- Prof Ravi CSE168
- TU WIEN Rendering
- PBRT3