辐射度量学

Energy 能量

单位焦耳，物理里最常见的符号之一。某个波长的光线能量实质上是含有光子的数量。一个光子所带的能量可以用以下公式来刻画，\(\lambda\)为波长,h为普朗克常数: \( Q = \frac{hc}{\lambda} \)

Flux

称为power(功率)，单位瓦特(w), 又可以被称为Radiant flux,单位流明(lm)。Flux可以通过能量对时间做微分得到

\[ \Phi = \frac{\text{d}Q}{\text{d}t} \]

一个在空间中的球形光源每单位时间内对周围360度空间内辐射的能量就是功率, 也就是Flux。

Irradiance

给定一个有限的面积, 我们可以得到单位时间内单位面积所得到的能量。

\[ E = \frac{Q}{At} = \frac{\Phi}{A} \]

考虑一个空间中的点光源，以它为圆心，处于半径r处的圆壳上所收到的单位时间，单位面积的能量为

\[ E = \frac{\Phi}{4 \pi r^2} \]

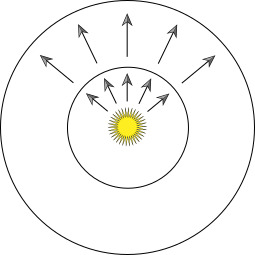
radiance

要理解radiance要先理解立体角，在二维的情况下圆只有一个角度\(\theta\)，在三维下有两个角度相对z轴的\(\theta\)和绕z轴旋转的\(\phi\)，立体角的单位是\(\omega\)。 radiance的符号是L，渲染中用的最多的符号，代表沿着某个单位立体角方向、单位时间、单位面积的光线强度。下式描述了在p点，沿着\(\omega\)立体角方向的radiance:

\[ L(p,\omega) = \frac{\text{d} E_\omega (p)}{\text{d}\omega} \]

由于立体角方向往往与面积所在的平面不垂直，所以还需要加上投影项\(\cos\).

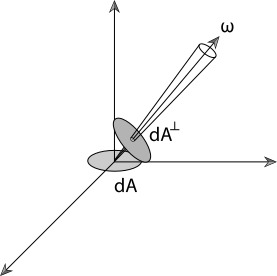
与\(\omega\)垂直的单位面积\(dA'\)大约是真实的\(dA\)(在xy平面)的\(\cos\theta\)倍(直观的想，当\(\omega\)方向与\(dA\)的法线平行的时候,此时dA = dA')。因此radiance可以被写作

\[ L(p,\omega) = \frac{\text{d}^2\Phi(p,\omega)}{\text{d}\omega \text{d}A \cos\theta} \]

渲染方程

BRDF与反射方程

BRDF(Bidirectional Reflectance Distribution Function),双向反射分布函数，刻画了由\(\omega_i\)方向进入的radiance,在点P处得到了irradiance后，沿着若干个\(\omega_o\)方向反射出去之间的比例关系。即每一个\(\omega_o\)方向的radiance与点p沿着\(\omega_i\)方向所进入的radiance之间的关系。

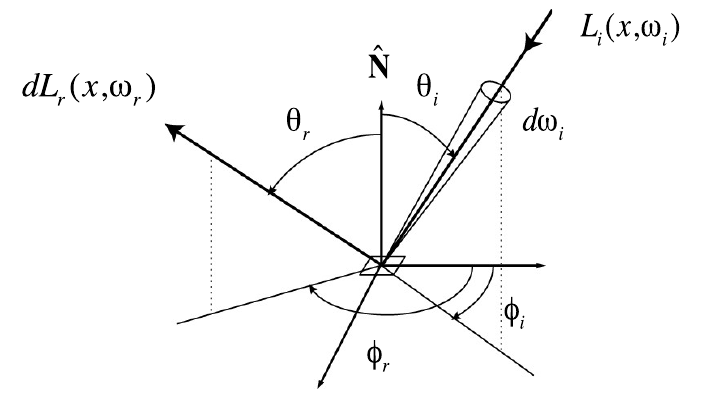
其中

\[ f_r(\omega_i \Rarr \omega_r ) = \frac{dL_r(\omega_r)}{dE_i(\omega_i)} = \frac{dL_r(\omega_r)}{L_i(\omega_i)\cos\theta_i d\omega_i} \]

有了上述的物理量以后，我们可以定义渲染方程了。首先，如果知道了一个点来自各个方向的radiance, 我们可以沿着所有方向对radiance进行积分，从而得出这个所在的点的*irradiance。

\[ L(p,\omega) = \cfrac{\text{d}^2\Phi(p,\omega)}{\text{d}\omega \text{d}A \cos\theta}\\ \rArr \\ L(p,\omega) = \cfrac{\text{d} E(p,\omega)}{\text{d}\omega \cos\theta} \\ \rArr \\ \text{d} E(p,\omega) = L(p,\omega)\cos\theta \text{d}\omega \]

在渲染的环境下，反射方程只考虑物体表面外的半球体的入射、反射，因此做半球积分，

\[ E(p) = \int_{\Omega^+} L_i(p,\omega)\cos\theta_i \text{d}\omega \]

我们关心的是相机方向收到的radiance，而不是点p收到的irradiance，所以在上式中加入BRDF项，得到反射方程。

\[ L_r(p,\omega_r)= \int_{\Omega^+} f_r(\omega_i \Rarr \omega_r ) L_i(p,\omega)\cos\theta_i \text{d}\omega \]

可以观察下图中，\(L_r\),\(L_i\)的方向

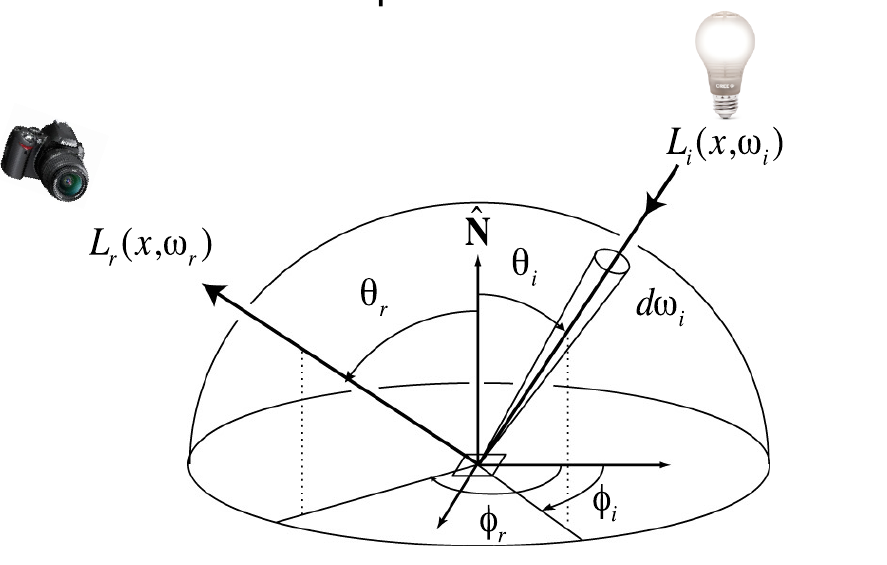
最后，物体是可以自发光的，所以以上公式还缺了一个发光项，由于我们假设了光线是线性可加的，因此直接加上就可以了

\[ L_r(p,\omega_r)= L_e(p,\omega_o) + \int_{\Omega^+} f_r(\omega_i \Rarr \omega_r ) L_i(p,\omega)\cos\theta_i \text{d}\omega\\ where: \cos\theta_i = \mathbf{n} \cdot \mathbf{w_i} \]

这个公式要注意，\(w_i\)在图中只是为了说明这是一个入射光，实际上在计算中，\(w_i\)的方向应从p点指向外面，否则\(\cos\)项会为负数。

这个方程中有循环定义，因为某一个方向的\(L_r\)依赖于另一个方向\(L_i\)，而\(L_i\)也是未知的，因为\(L_i\)实质上也是从其他方向进来的\(L\)所得到的。所以很遗憾，这个式子是没有解析解的，只能得到数值解, 解这个式子最常用的方法是蒙特卡罗积分，最常见的实现是路径追踪。

Reference

闫令琪 GAMES101 课件14,15
PBRT v3

辐射度量学与渲染方程