Cook-Torrance反射方程
原始的Cook-Torrance反射方程来自论文1. (注:原文的公式里的分母少了一个4) \( \begin{aligned} &L_{o}\left(p, \omega_{o}\right) =\int_{\Omega^+}\left(k_{d} f_d(\omega_i \rArr \omega_o)+ k_{s}f_{s}(\omega_i \rArr \omega_o)\right) L_{i}\left(p, \omega_{i}\right) (n \cdot \omega_{i}) d \omega_{i}\\ \text{where:}\\ &f_d(\omega_i \rArr \omega_o) = \textcolor{red}{\frac{c}{\pi}}\\ &f_s(\omega_i \rArr \omega_o) = \frac{D F G}{4\left(\omega_{o} \cdot n\right)\left(\omega_{i} \cdot n\right)}\\ &k_d + k_s = 1 \end{aligned} \)
Info
- 为什么标红了\(f_d\)?
这里是在微表面模型上补充了一个diffuse项,因为微表面模型是一个纯的specular的模型,并且通常我们渲染的时候只考虑在表面进行单次弹射。所以在非常粗糙的表面(意味着表面的沟壑越多),光线被遮挡的几率越高,能量会有损失。加一个diffuse项可以代偿这个能量的损失,尤其是在粗糙度高的表面。
对GGX的白炉测试如下图,可以见到随着roughness升高,能量损失越明显。

- 这么做对吗?
首先可以明确的说,加一个diffuse项是绝对不符合物理的。
从直观来理解,一个表面不可能既是diffuse,又是specular的。
虽然通过一个\(ks + kd = 1\)来维持了能量守恒,但是这相当于从diffuse项为specular损失的部分凑了能量。
其次,这里选择的\(f_d\)是一个lambertian的brdf,是不随着roughness变化的一个brdf,更真实的diffuse应该随着roughness而发生变化。
- 正确的做法
在specular项损失能量的原因是因为只有单次反射,光线单次反射以后没有被我们观察到,所以能量损失了。直观的思路是进行多次弹射,直到我们观察到为止。在实现上,我们需要在\(f_s\)这个单次弹射的brdf上再叠加一个\(f_{ms}\)的brdf代表多次弹射用于弥补能量损失。
以上提到方法是kulla-conty方法, 实现见Google的filament。23
经过能量补偿的GGX白炉测试。

DFG的选择
常用的D,F,G函数有多个选择。
菲涅尔反射项
F项我们可以选用schilick近似。F函数描述了光线在经过某个物体表面的反射率和折射率。F函数中的\(F_0\)项描述了光线以0度的偏差(沿着法线方向)碰撞表面的时候的反射率,电介质这个值很低。那么剩下的\(1 - F_0\)就是发生
折射的能量。
如果把角度和微表面模型考虑进去,那么在Cook-Torrance中,它会形如
\[ F_{Schlick}\left(h, v, F_{0}\right)=F_{0}+\left(1-F_{0}\right)(1-(h \cdot v))^{5}\labeltag{1} \]
注意该函数 \(\eqref{1}\) 是关于\(h,v\)的函数,其中\(h\)需要格外注意。
在
Fig. 电介质菲涅尔项dielectric物体中,从0度看过去的初始反射率\(F_0\)比较低,只有到接近\(90\degree\)的时候形成grazing angle,反射率会大幅提高, 关注下图的下面曲线。
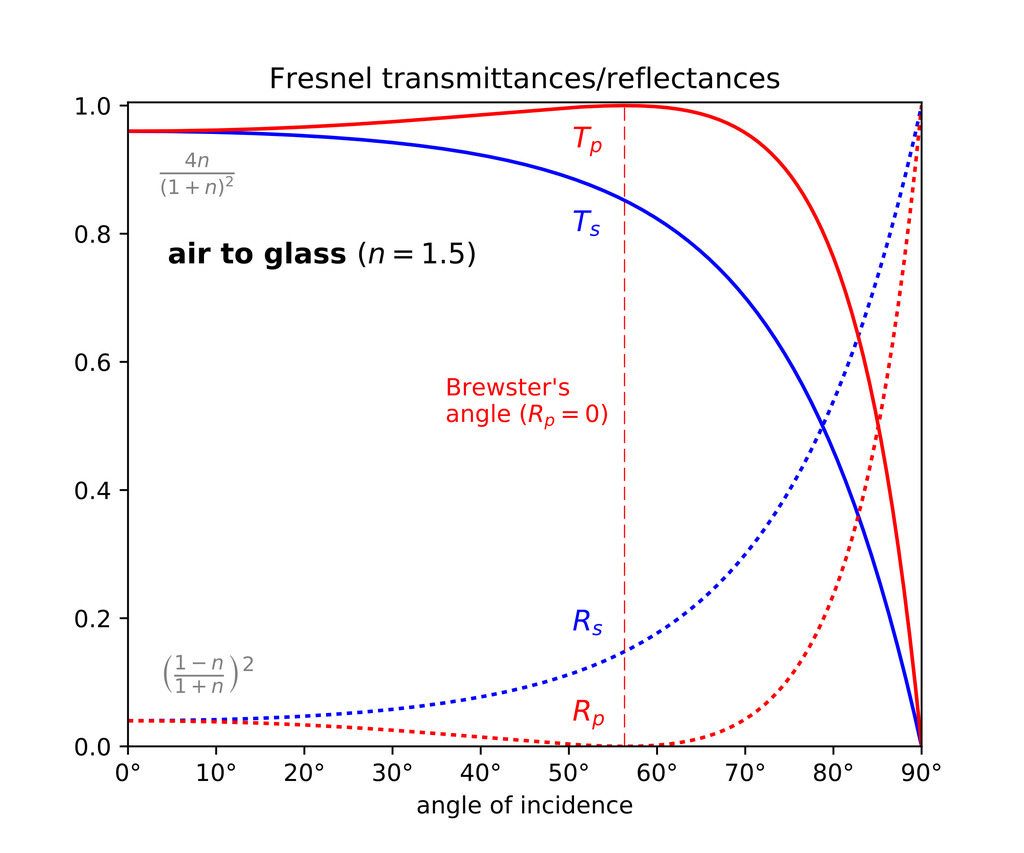
而对于
Fig. 导体的菲涅尔项conductor,比如金属,他们的初始反射率就比较高,但是仍然会形成grazing angle。
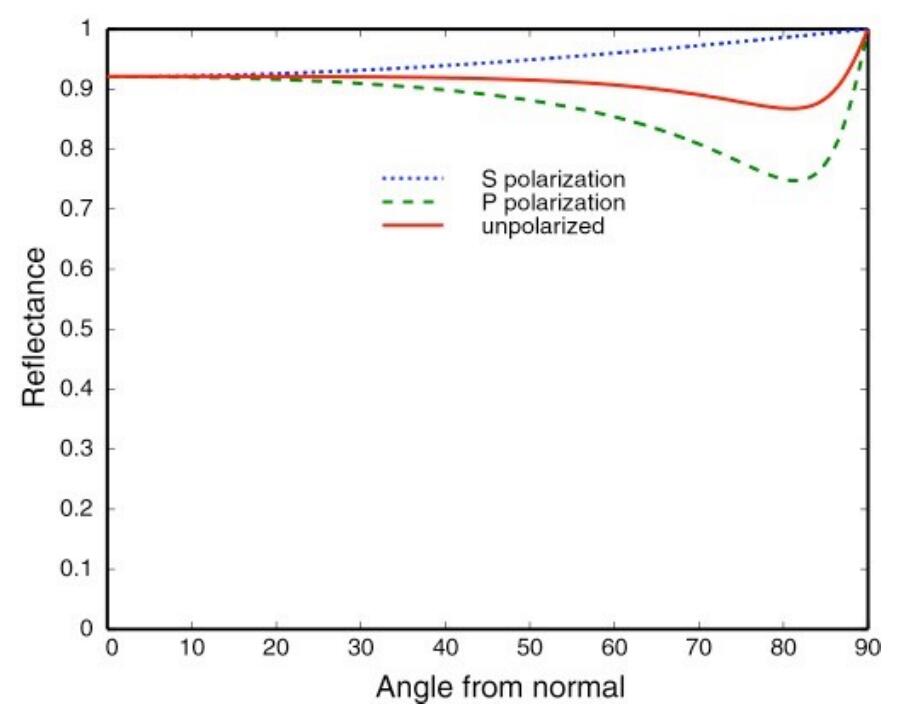
法线分布函数(NDF)
NDF函数描述了微表面模型的法线分布,在给定\(n \cdot h\)和粗糙度\(\alpha\)下,其反映了当前模型上有多少微表面的法线与给定输入\(h\)重合。关于它的选择有很多,常用的包括Trowbridge-Reitz GGX函数。它是形如
\[ NDF_{GGX}(n, h, \alpha)=\frac{\alpha^{2}}{\pi\left((n \cdot h)^{2}\left(\alpha^{2}-1\right)+1\right)^{2}}\labeltag{2} \]
有一点需要格外注意,函数\(\eqref{2}\)是有关\(h\)的一个函数。并且所有的NDF都遵循一个性质: 如果给定一个点,已知它的法线和粗糙度,那么
\[ \int_{\Omega} D(h) \cos \left(\theta_{h}\right) d \omega=1 \]
这个式子隐含了一个重要的推论:所有的NDF乘以cosine项都代表了一个pdf函数。这意味着GGX的pdf函数就是
\[ pdf_{ggx}(n,h,\alpha) = \frac{\alpha^{2} (\mathbf{n} \cdot \mathbf{h})}{\pi\left((n \cdot h)^{2}\left(\alpha^{2}-1\right)+1\right)^{2}} \]
这个推论会帮助后续对brdf进行重要性采样。对这个pdf积分,进行逆变换采样得到
\[ \theta=\arccos \sqrt{\frac{1-r_1}{r_1\left(\alpha^{2}-1\right)+1}} \\ \phi = 2\pi r_2 \]
拿到球面坐标后转到x,y,z坐标就可以拿到向量\(\mathbf{h}\)的笛卡尔坐标系表达。 注意,我们所采样的\(\theta\),\(\phi\)都是关于\(h\)向量的。所以\(pdf\)也是关于\(\mathbf{h}\)向量的,我们实际关心的是\(w_o\)方向的pdf。因此要把\(p(h)\)转换到\(p(w_o)\),涉及到一点jacobian。
具体的证明可以见Bruce Walter的论文4。 不过简单的描述下,因为\(h\)是半程向量,所以\(\theta_h^* \)是\(\theta_o^*\)的二分之一。后面的分子的\(\sin\theta_h\)是因为把笛卡尔坐标系的x,y,z转变到球面坐标系需要乘以\(\sin\theta_h\),计算完了以后要回到笛卡尔坐标系,从球坐标回到笛卡尔坐标系需要除以\(\sin\theta_o\)。
\[ \begin{aligned} p_{o}(\mathbf{o}) &=p_{h}(\mathbf{h})\left\|\frac{\partial\left[\theta_{h}^{\star}, \phi_{h}^{\star}\right]}{\partial\left[\theta_{o}^{\star}, \phi_{o}^{\star}\right]}\right\| \frac{\sin \theta_{h}^{\star}}{\sin \theta_{o}^{\star}} \\ &=p_{h}(\mathbf{h})\left|\frac{1}{2}-0\right| \frac{\sin \theta_{h}^{\star}}{\sin 2 \theta_{h}^{\star}} \\ &=\frac{p_{h}(\mathbf{h})}{4 \cos \theta_{h}^{\star}}=\frac{p_{h}(\mathbf{h})}{4(\mathbf{h} \cdot \omega_o)}\\ &=\frac{D(n,h,\alpha)(\mathbf{n} \cdot \mathbf{h})}{4(\mathbf{h} \cdot \omega_o)} \end{aligned} \]
作图可视化,巧合的是NDF的形状恰好类似于正态分布,名字也比较像:)。
GGX是一个二维的函数,输入域包括\((n \cdot h)\)和\(\alpha\)两个变量,作图的时候需要固定住\(\alpha\)。
其形状类似于正态分布,在\((n \cdot h) \approx 0\),也就是接近镜面反射的时候值比较大,这是实现glossy材质的关键。
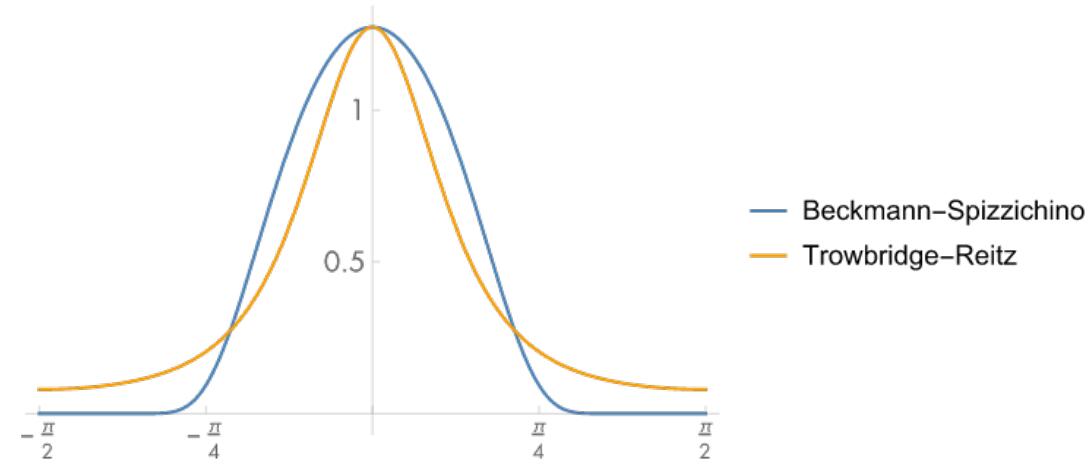
Fig. GGX和BeckmanNDF对比,横轴为h与n夹角
GGX的曲线更平滑,意味着在渲染中高光边缘更加的平滑
几何遮蔽项G
几何遮蔽项\(G\)描述了表面的自遮挡程度。当光线以0度直射表面的时候,其自遮挡应该接近于0,而当接近grazing angle的时候, 其自遮挡应该有明显提高。几何遮蔽项描述了自遮蔽后的能量强度。
其通常可以拆分为两部分,光线被遮挡的部分(shadowing)和视线被遮挡的部分(masking)。
一个可以选择的G的公式为schlick-GGX近似,其形如
\[ G_{ggx}(n, v, k)=\frac{n \cdot v}{(n \cdot v)(1-k)+k} \]
其中\(k\)是一个和粗糙度roughness有关的常数。
一个完整的G函数由两部分组成:
\[ G(n, v, l, k) \approx G_{ggx}(n,v,k) G_{ggx}(n,l,k)\labeltag{3} \]
其可视化可以见5
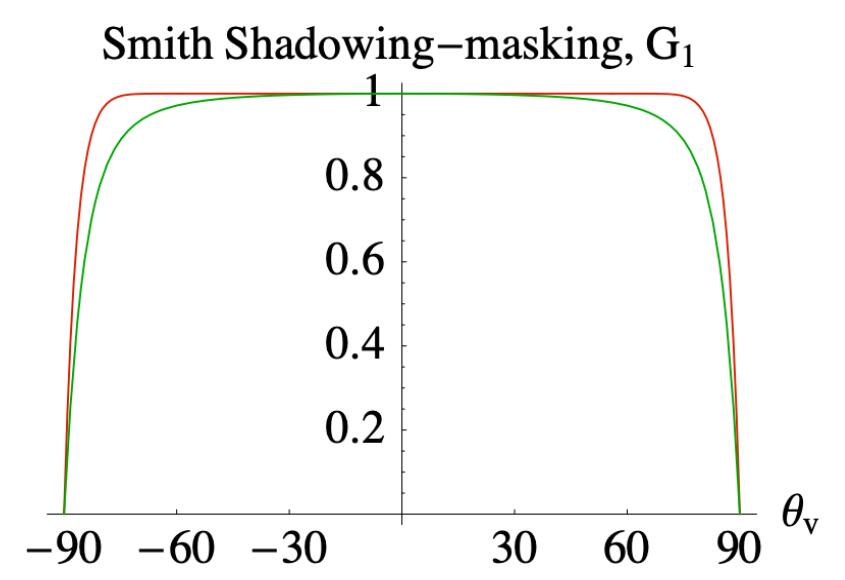
Fig. 几何遮蔽项函数图
红色为Beckmann分布,绿色为GGX分布
可以观察到,除了接近grazing angle的时候,其他时候G项都接近于1,代表所有能量都没有被遮挡。
另外一个可以值得注意的,在接近grazing angle的时候,BRDF的分母有一个\((N \cdot V)\)接近于0,如果分子没有一个\((N \cdot V)\)做抵消,那么在grazing angle的地方会因为brdf无穷大而开始发光。如果渲染球体的时候G项有bug,那么球的边缘会有明显的一圈白光。
Diffuse(Diffuse Irradiance Map)
如果不用kulla-conty方法补能量的话,直接加个diffuse项虽然不科学但是还是可以搞,至少不会一眼穿帮。
关于Diffuse部分如何近似有很多方法,可以用黎曼积分求解,或者蒙特卡洛方法求解(cosine weigted sampling),也可以用球谐函数来近似。具体的可以看详解Cubemap、IBL与球谐光照介绍的求解方法。
Specular 两次Split Sum
分离光照和BRDF(pre-filtered environment map)
第一次拆积分是发生在渲染方程中,我们将光照项\(L_i(p,\omega_i)\)和brdf项拆开。
\[ \begin{aligned} L_{o}\left(p, \omega_{o}\right) &=\int_{\Omega^+}\left(f_r(p,\omega_i \rArr \omega_o)\right) L_{i}\left(p, \omega_{i}\right) (n \cdot \omega_{i}) d \omega_{i}\\ &\approx \int_{\Omega^+}\left(f_r(p,\omega_i \rArr \omega_o)\right) (n \cdot \omega_{i}) d \omega_{i} \times \frac{\int_{\Omega^+}L_{i}\left(p, \omega_{i}\right)(n \cdot \omega_{i}) d \omega_{i}}{\int_{\Omega^+}(n \cdot \omega_{i}) d \omega_{i}}\\ \text{Monte Carlo Method}:\\ &\approx \frac{1}{N_1}\sum_{1}^{N_1}\frac{f_r(p,\omega_i \rArr \omega_o)(n \cdot \omega_{i})}{pdf(n,\omega_o,\alpha)} \times \frac{\frac{1}{N_2}\sum_{1}^{N_2}\frac{L_{i}\left(p, \omega_{i}\right)(n \cdot \omega_{i})}{pdf}}{\frac{1}{N_2}\sum_{1}^{N_2}\frac{n \cdot \omega_{i}}{pdf}}\labeltag{4} \end{aligned} \]
等式\(\eqref{4}\)的后半部分上下采样同种采样方式和采样数量,因此pdf和\(N_2\)可以约去,化简为
\[ \frac{\sum_{1}^{N_2}L_{i}\left(p, \omega_{i}\right)(n \cdot \omega_{i})}{\sum_{1}^{N_2}n \cdot \omega_{i}}\labeltag{5} \]
通过mipmap配合,我们可以对一个环境光照的cubemap进行不同粗糙度和分辨率的预积分。roughness越高,其prefiltered的结构越糊,放到mipmap的分辨率更小,在采样的时候可以在不同mipmap上进行插值。
计算prefiltered envmap
与BRDF为常数的diffuse情况不同,specular部分涉及到复杂的BRDF,所以可以根据BRDF的分布(主要是NDF函数的分布)进行重要性采样,对不同NDF的采样推导可以见Importance Sampling techniques for GGX with Smith Masking-Shadowing: Part 1和Sampling microfacet BRDF两篇文章,常读常新。同时,NDF函数\(D\)是一个与半程向量\(h\)有关的函数,半程向量\(h\)与视角方向\(V\)有关,在预积分的时候我们并不知道视角方向\(V\),因此做一个假设\(V\)与法线同向(引入了误差,导致glazing angle的锐利反射丢失),则\(V = R = N\)。
通过以上假设,知道了每一个像素的法向量\(N\)和\(V\)。通过GGX重要性采样获取半程向量\(H\)。有了H和V以后我们可以计算出L的方向,有了L方向以后就可以在cubemap上进行texture查询了。
虽然式子\(\eqref{5}\)中不包含roughness,但是在以上提到的实现中需要用到GGX重要性采样,而GGX的重要性采样公式\(\eqref{2}\)里包含了roughness项。
这部分代码见prefilter.frag
Info
- 为什么可以拆积分?
一个还不错的解释见Paper for the approximation formula provided by Brian Karis
如果我们考虑光源是来自周围恒定的radiance,比如白炉测试的环境,那么光源的Radiance(\(L_i\))是个常数,从积分里拆出来一个常数项是完全等价的。如果将环境光照假设其携带的是低频信息(较为均匀的光照),这样拆积分不会损失太多的信息(会丢失高频信息)。
- 式子\(\eqref{4}\)的第二步拆出的积分项为什么上下有\((n \cdot \omega_i)\)?
Epic的公式推导里并没有写cosine,但是shader代码里有。脚注里语焉不详, 仅仅说加了cosine效果会更好。
自己的思考:cosine项起了一个加权平均的效果。\(L_i\)对最终的irradiance的贡献与其入射角度有关系。

Fig. 1:不同粗糙度下的预计算环境光源积分
split BRDF
采用schlick近似,可以将渲染方程拆分为
\[ F_{0} \int_{\Omega} \frac{f_{r}\left(p, \omega_{i}, \omega_{o}\right)}{F_{schlick}}\left(1-\left(1-\omega_{o} \cdot h\right)^{5}\right) n \cdot \omega_{i} d \omega_{i}+\int_{\Omega} \frac{f_{r}\left(p, \omega_{i}, \omega_{o}\right)}{F_{schlick}}\left(1-\omega_{o} \cdot h\right)^{5} n \cdot \omega_{i} d \omega_{i} \]
注意到BRDF内\(fr()\)本身含有frenel项,所以其分子只剩下\(D(n,h,\alpha),G(n,v,k)\)项。当采用重要性采样的时候(\(D\)乘以cos即为pdf)做蒙特卡洛积分的时候需要除以pdf,因此D项被消去,分子只剩下\(G(n,v,k)\)项,其中\(k\)是\(\alpha\)的函数,\(\omega_o\)是\(v\)的另一个记号。
\(F_0\)是常数,法线\(N\)已知。在蒙特卡洛积分的过程中通过采样获取\(H\),已知\(V\)可以算出\(L\),也就是\(\omega_i\),式子中全部符号现在均已知。
该式子可以打表,其只与\(n \cdot v\)和\(\alpha\)有关,因此可以打表为二维纹理,代码见precompute_brdf.frag。
最后合并两个splitsum的结果可以写作(摘抄自LearnOpenGL),再加上diffuse的部分(或者kulla-conty补的能量)就完成了。
float lod = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
总结
MC为蒙特卡洛方法。
- Cook, Robert L., and Kenneth E. Torrance. "A reflectance model for computer graphics." ACM Transactions on Graphics (ToG) 1.1 (1982): 7-24. ↩
- Revisiting Physically Based Shading at Imageworks ↩
- Filament: Energy loss in specular reflectance ↩
- Walter, Bruce. "Notes on the Ward BRDF." Program of Computer Graphics, Cornell University, Technical report PCG-05 6 (2005). ↩
- Walter, B., Marschner, S. R., Li, H., & Torrance, K. E. (2007). Microfacet Models for Refraction through Rough Surfaces. Rendering techniques, 2007, 18th. ↩
- Real Shading in Unreal Engine 4 ↩
- Specular IBL,learnopengl ↩