• 菲涅尔项 描述了以某个角度看向微表面有多少能量被反射。
• NDF项，描述了微观法线的统计分布。给定参数粗糙度，法线和半程向量h，NDF给出了整个微表面朝向h的统计分布。
• G项是一个0,1之间的量，给定法线n,观测角度v和粗糙度，返回有多少比例的面可以同时被入射方向和出射方向观察到，通常来说这个值约等于1，只有在接近glazing angle的时候，会大幅减少，因为此时接近于平视微表面，有大量的面被遮挡。

能量损失

来自filament.

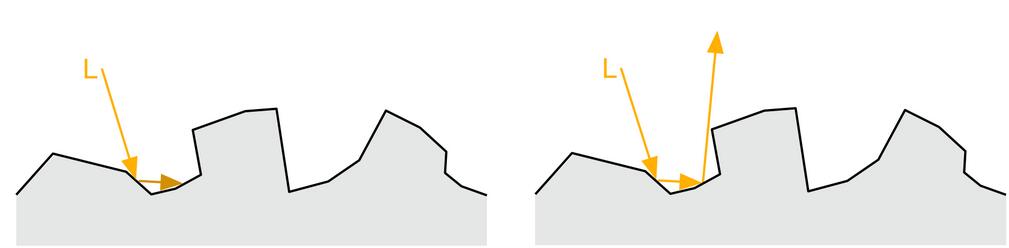
在建模BRDF的时候只考虑了单次弹射，没有考虑多次反射，在高粗糙度的表面容易有能量损失。 直观理解就是在高粗糙度的时候G项会更接近于0。

能量补偿

Kulla2017提出可以通过额外的近似项来补偿损失的能量。

• 先进行白炉测试，假设从四面八方入射的radians都是1，并且假设物体的表面F0为1,进行积分后打表。反应了在给定粗糙度和\(\cos \theta\)上的出射能量。
• 构造一个新的brdf，使得它的积分结果为\(1 - E(u)\).
• 把新的brdf加到原来的brdf上。

详细推导 (to be continued)