渲染方程的解析解
(注:这部分来着Prof Ravi的CSE168 Homework2)
渲染方程的完整形式,其中假定 \(\omega_i\) 是指向光源的,\(\omega_o\) 指向视角方向,符号 \(V\) 包含光线的可见性。
\[ \textcolor{red}{L_r(p,\omega_r)} = \textcolor{blue}{L_e(p,\omega_o)} + \int_{\Omega_P} \textcolor{blue}{f_r(\omega_i \Rarr \omega_r )}\textcolor{red}{ L_i(p,\omega)} \textcolor{blue}{\cos\theta_i \textcolor{blue}{V(\omega_i)} \text{d}\omega_i}\\ where: \cos\theta_i = \mathbf{n} \cdot \mathbf{w_i} \]
如果我们不考虑自发光项,忽略光线传播中的被遮挡情况(意味着没有阴影),着色表面Lambert漫反射的时候,公式可以简化为如下,其中漫反射brdf为常数,\(f = \frac{k_d}{\pi}\) , \(k_d\)往往为物体颜色的RGB分量。
\[ L_r(\bm \omega_o) = f \int\limits_{\Omega_P} (\bm n \cdot \bm \omega_i) L_i d\bm \omega_i. \]
上式的积分部分被称为irradiance(radiance沿着立体角积分为irradiance),其积分区域为多边形光源\(P\),多边形光源由\(n\)个顶点 \(v_1,v_2,\cdots,v_n\)构成。
我们可以引入一个新的记号\(\Phi\)记作irradiance vector,多边形光源\(P\)给点r带来的irradiance vector可以写作
\[ \bm \Phi(r) = \frac{1}{2}\sum_{i=1}^{n}\Theta_i(r)\bm \Gamma_i(r), \tag{0} \]
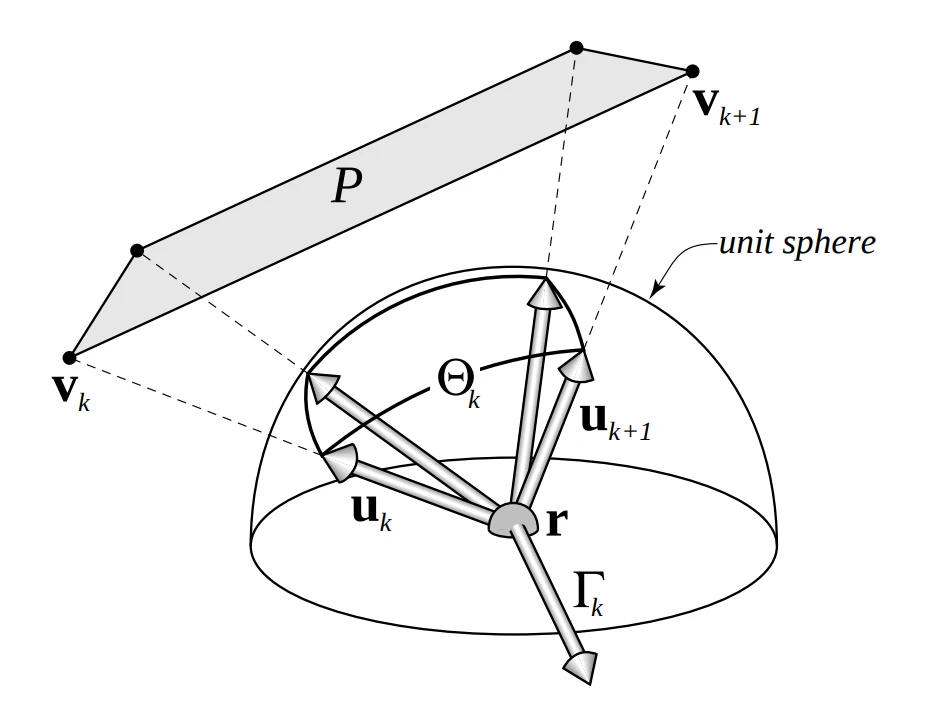
\(\Theta_k(r)\) 和 \(\bm \Gamma_k(r)\) 分别计算如下 \( \Theta_k(r) = cos^{-1}\bigg(\frac{\bm v_k-\bm r}{\lVert\bm v_k-\bm r\rVert}\cdot\frac{\bm v_{k+1}-\bm r}{\lVert\bm v_{k+1}-\bm r\rVert}\bigg) \)
\[ \bm \Gamma_k(r) = \frac{(\bm v_k-\bm r) \times (\bm v_{k+1}-\bm r)}{\lVert(\bm v_k-\bm r) \times (\bm v_{k+1}-\bm r)\rVert} \]
而标量的irradiance可以从irradiance vector和法向量的积分求得(注意带正负),\(\bm \Phi(r) \cdot \bm n(r)\),也可以展开写成这种形式:
\[ \bm \Phi(r) \cdot \bm n(r)=\frac{1}{2} \sum_{i=1}^{n} \operatorname{acos}\left(p_{i} \cdot p_{j}\right)\left(\frac{p_{i} \times p_{j}}{\left\|p_{i} \times p_{j}\right\|} \cdot\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right]\right) \]
带入渲染方程可以解出渲染方程的解析解
\[ L_r(\bm \omega_o) = f L_i * (\bm \Phi(r) \cdot \bm n(r)) = \frac{k_d}{\pi} L_i * (\bm \Phi(r) \cdot \bm n(r)). \tag{4} \]
以上这部分的详细推导可以见Heitz的Geometric Derivation of the Irradiance of Polygonal Lights。
但是其irradiance vector的表述略有不同,按我的理解irradiance * brdf = radiance。但是Heitz的表述里把lambertian的BRDF的归一化的系数\(1/\pi\)放进了irradiance vector的分母里,而在实际计算\(L_r\)的时候只乘了\(k_d\),其数学结果是一样,只是我认为Ravi的记号更易理解一点。
路径追踪(光源采样,16spp,无间接光,不考虑遮挡)和解析解的对比,注意右侧由蒙特卡洛方法带来的采样噪点和下方无阴影。

Fig. 解析解和数值解比较
shadertoy demo可以见demo
LTC方法的面光源渲染
关键思想
- 最左侧是一个cosine分布,通过一个\(3\times3\)的矩阵\(M\),可以变换到任意形状的球面分布,最典型的就是BRDF的分布。其中对角线的元素控制
roughness,不均一的大小可以控制各向异性,副对角线的元素可以控制BRDF的skewness,动图见https://eheitzresearch.wordpress.com/415-2/
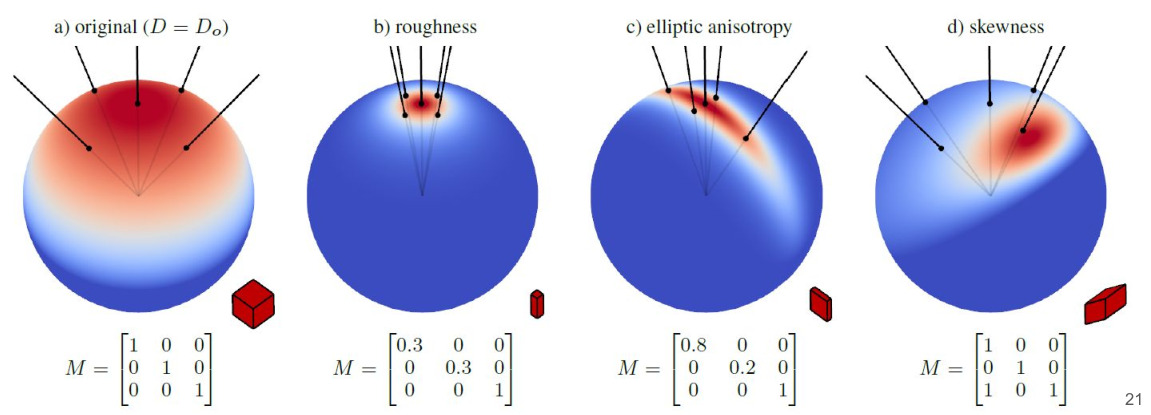
Fig. 不同矩阵M对cosine分布的形状改变
- 通过同样的M矩阵可以变换光源的坐标位置以改变光源的形状
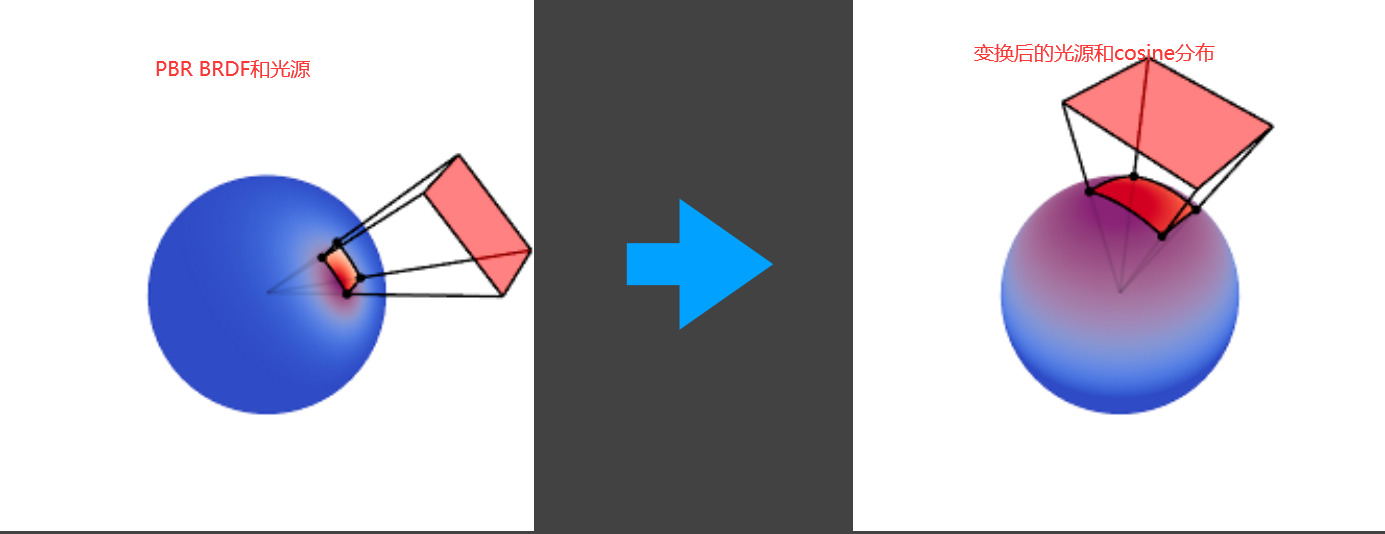
Fig. 光源和分布共同变换
- 变换后的光源和cosine分布有解析解
设\(\omega\)为BRDF lobe的某个向量,\(\omega_o\)是cosine分布的某个向量,\(D(\omega)\)为BRDF分布,\(D(\omega_o)\)是cosine分布。存在某个矩阵\(\mathbf{M}\)有以下关系
\(\omega = \frac{M\omega_o}{||M\omega_o||}\)。
概率分布的转换需要jacobian项,其jacobian项的推导可以见原文,其分布的变换可以写作
\[ D(\omega)=D\left(\omega_{o}\right) \cdot \frac{\partial \omega_{o}}{\partial \omega}=D\left(\frac{M^{-1} \omega}{\left\|M^{-1} \omega\right\|}\right) \cdot \frac{\left|M^{-1}\right|}{\left\|M^{-1} \omega\right\|^{3}} \]
也可以写作如下(官方的代码是这样写的,没纸笔推)
\[ D(\omega)=D\left(\omega_{0}\right) / \frac{\partial \omega}{\partial \omega_{o}}=D\left(\frac{M^{-1} \omega}{\left\|M^{-1} \omega\right\|}\right) / \frac{\left|M\right|}{\left\|M \omega_o\right\|^{3}} \]
积分区域\(P_o = M^{-1}P\),推出下式
\[ \int_{P} D(\omega) d \omega=\int_{P_{o}} D_{o}\left(\omega_{o}\right) \cdot \frac{\partial \omega_{o}}{\partial \omega} d \omega=\int_{P_{o}} D_{o}\left(\omega_{o}\right) d \omega_{o} \]
所以证明在\(P\)区域对分布\(D(\omega)\)的积分等于在经过某个变换后的\(P_o\)区域上的\(D(\omega_o)\)。
因此我们可以把复杂的BRDF Lobe转到有解析解的cosine分布上,从而获得其解析解。问题是寻找其变化关系\(M\)。
变换矩阵M的定义与寻找
考虑到矩阵\(M\)的主对角线元素控制roughness和各向异性,副对角线元素控制BRDF的偏斜程度,m33必须始终为1,因为着色坐标系在局部坐标系下,BRDF Lobe是绕着Z轴对称的。
待拟合的球面分布\(D(\omega)=f(\vec{l},\vec{v})\cos(\theta)\),用于拟合的分布为截断cosine分布\(D(\omega_o)=\cos(\theta_o)\)
M的形式如下
\[ M=\left[\begin{array}{lll} a & 0 & b \\ 0 & c & 0 \\ d & 0 & 1 \end{array}\right] \]
我们在渲染过程中关心的是从BRDF Lobe转到cosine分布,也就是\(M^{-1}\),其代数形式可以写作,需要保存5个元素。
\[ M^{-1}=\left[\begin{array}{ccc} c & 0 & -b c \\ 0 & a-b d & 0 \\ -c d & 0 & a c \end{array}\right] /(ac- bcd)=\left[\begin{array}{ccc} 1 & 0 & -b \\ 0 & (a-b d) / c & 0 \\ -d & 0 & a \end{array}\right] /(a - bd) \]
在后续的改进中,在拟合过程中对求得的\(M\)矩阵的中间元素进行归一化并调整其他行以保证行列式不变,代码变更具体可以见diff。
因为对右下角的元素进行归一化的话,会出现数值不稳定的现象,这在Bilinear texture采样的时候会有问题,因此最初的实现中是保存了5个元素,在shader中进行实际的归一化。
Fig. 以右下角元素归一化的Minv矩阵
后续改进发现以中间的元素进行归一化的数值稳定性更好,只用保存四个角的四个元素(然而仍然需要第二章纹理来保存菲涅尔项,所以也不是那么的有用)。
\[ M=\left[\begin{array}{lll} a & 0 & b \\ 0 & 1 & 0 \\ c & 0 & d \end{array}\right], M^{-1}=\left[\begin{array}{ccc} d & 0 & -b \\ 0 & 1 & 0 \\ -c & 0 & a \end{array}\right] /(ad - bc) \]
拟合的过程用的Nelder–Mead方法,用于在多维空间内搜索目标函数的最小值,用于对导数不可知的目标函数进行搜索,但是其对初值比较敏感。其拟合过程大致是猜一个M值,并对BRDF Lob和\(M*cos\)进行采样以比较其差异,计算loss。
计算的结果\(M^{-1}\)存放在以roughness和NdotV为uv坐标的纹理中,在着色的时候需要查表以将不同视角和粗糙度的BRDF转换到cosine分布中。
实现细节
菲涅尔项
这部分没有细看,和split-sum的方法有点像,因为预积分不能考虑过多的东西(纹理维度有限),所以把菲涅尔项从式子里抽出来单独处理。
菲涅尔项采用snell近似可以拆成两项,计算出来存放到另外一个纹理中并对积分的结果进行缩放即可。
裁剪
经过\(M^-1\)变换后的光源可能部分或者完全落在着色半球的下半圆部分,这部分应该被裁减掉,不然会出现错误的光照结果(比如光照不到的地方莫名其妙被着色了)。 裁剪可能需要新加入顶点(考虑一个正方形一个顶点在下方的情况,对一个顶点进行裁剪会多出一个顶点)。
这张图原图不是用来说明这个问题但是它画的挺好的。这张图本来是介绍一种无须裁剪的近似模型,但是没细看。
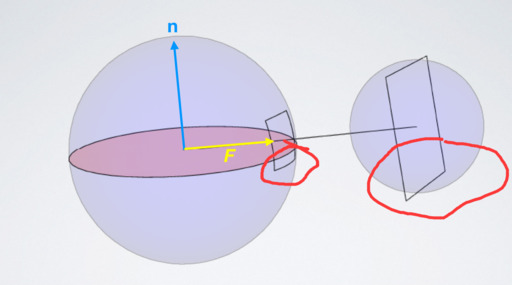
Fig. 面光源裁剪,红色区域为需要被裁剪部分
纹理
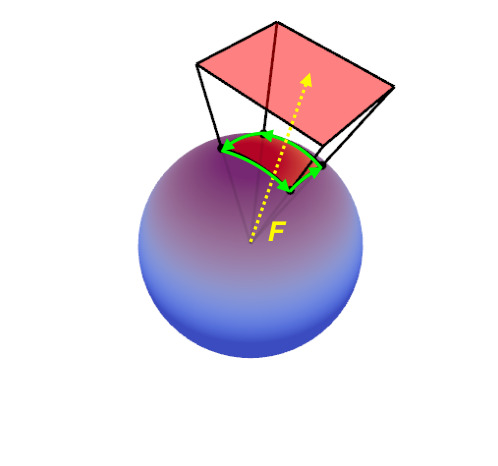
Fig. irradiance vector作为纹理采样方向
通过上文提到的irraidance vector的方向进行纹理采集(很好的性质,它必定和光源相交)。
纹理预先通过mipmap或者预计算的方式进行模糊,越粗糙的表面采样越模糊的纹理。采样的Lod选取与光源大小\(A\)和到光源的距离\(r^2\)有关系
float d = abs(planeDist) / pow(planeAreaSquared, 0.25);
float lod = log(2048.0*d)/log(3.0);//magic
float lodA = floor(lod);
float lodB = ceil(lod);
float t = lod - lodA;
//不同的mipmap上线性插值
vec3 a = FetchColorTexture(Puv, lodA);
vec3 b = FetchColorTexture(Puv, lodB);
return mix(a, b, t);
