Note
文章内图片来自参考资料1的课件。
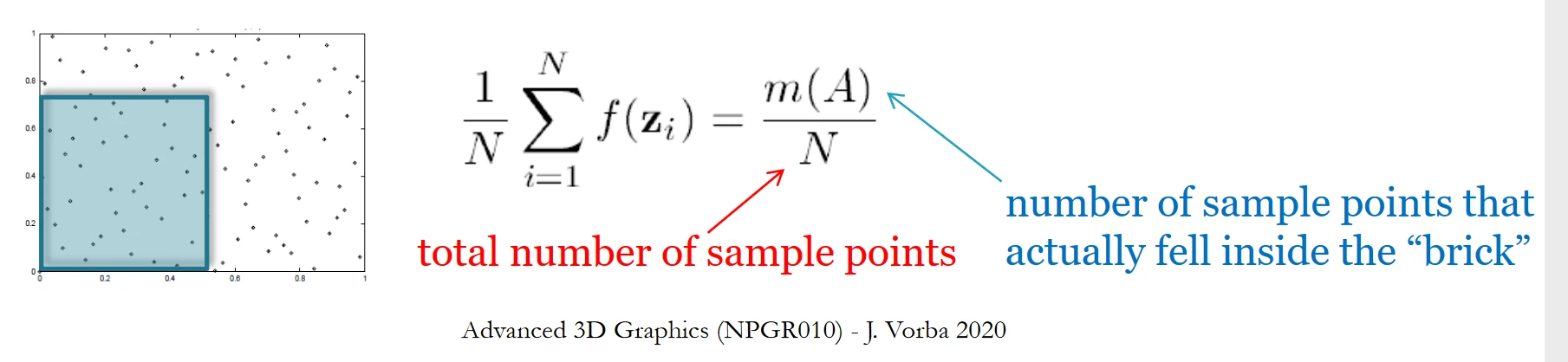
从N维空间任取一块空间,
- 这块空间和整体空间的比值 [0,1]
- 落在这块空间里的点和所有采样点的比值
任取一块空间,所有取的空间上面两个值的最大绝对差值就是"差异" 假设完全均匀分布(格子状),那么差异应该接近0。
Van Der Corput 序列
以2为底的序列
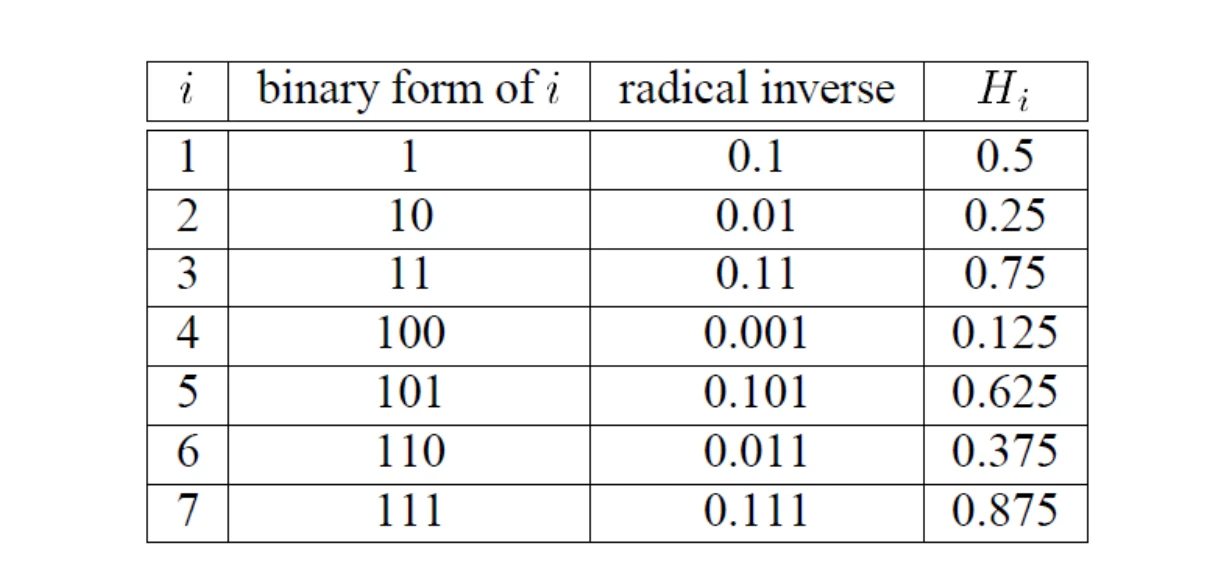
以2为底的表示有快速算法,观察其二进制表示,可以观察到其radical inverse是二进制位彻底翻转,然后前面加0.(相当于除以一个2^(n)次幂, n为表示这个数需要的二进制位)。
比如
100 = 4 --radical invese--> 001 = 1
转换为(0.001)_2 = 1 / 8
所以以2为底的VDC序列有一个快速的移位算法
float radicalInverse_VdC(uint bits) {
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
这个初看很复杂,但是实际上很简单..实质上就是分治法
- bits = (bits << 16u) | (bits >> 16u); 交换前16个bit和后16个bit
- bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u); 交换奇数bit和偶数bit
- bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u); 每两个bit交换位置
每4个bit交换位置 每8个bit交换位置(此时彻底完成了所有bit的位置反转)
然后再填加开头的(0.),实质上相当于乘以( 1 / (2^32)) = 2.3283064365386963e-10;
PBRT给了一个64位reverse的函数,换汤不换药,就是这个函数的变体,多移位一次。
以10为底的序列
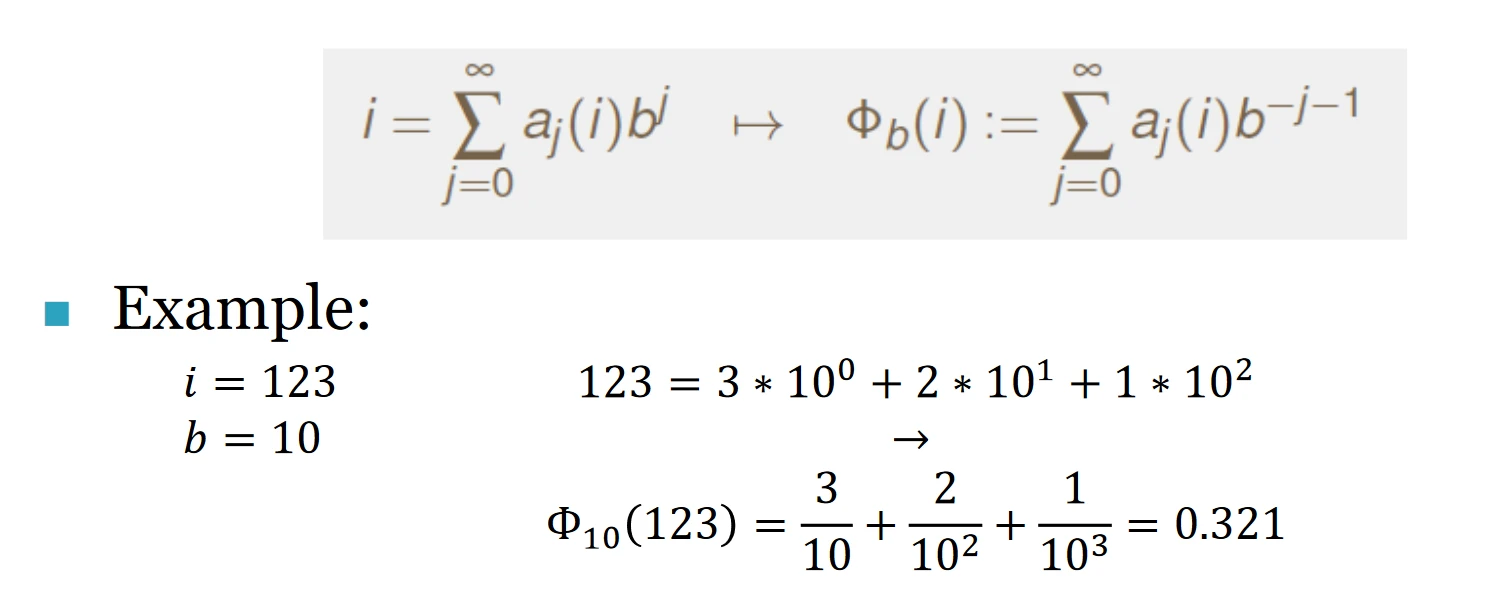
通用代码

Halton
halton和hammersley类似,只是halton是用两个不同底数(要求为互质的两个数,通常是质数,比如halton_2_3)组成序列。
Halton序列的问题: 底数选取较大的时候会出现明显的Pattern,尤其是多维的情况下。
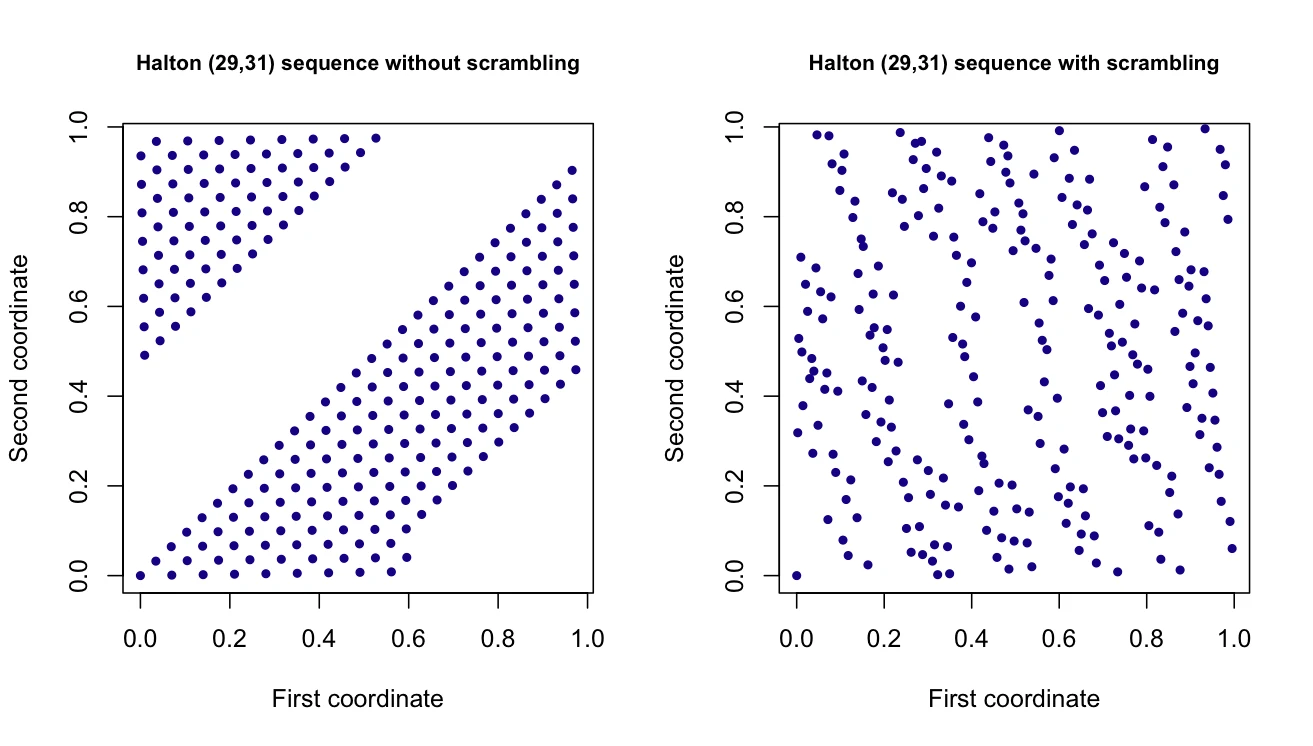
从VDC序列的性质可以知道,底数越大,那么就需要更多的数才能进到下一位。
假如我们有一个 VDC_57,以57为底数。那么根据公式简单推算,前57个点都均匀分布在[0,1]上,直到第58才会进位。
| 十进制数 | ||
|---|---|---|
| 1 | 1 * 57^0 | 1 / 57 |
| 2 | 2 * 57^0 | 2 / 57 |
| ... | ... | ... |
| 56 | 56 * 57^0 | 56 / 57 |
| 57 | 0 * 57^0 + 1 * 57 ^ 1 | 0 / 57 + 1 / 57^2 |
所以VDC序列的一个问题就是底数越大,那么规律性越强,Pattern越明显。
Scramble
以VDC_57为例子,再仔细观察Pattern出现的原因,我们会发现前57个采样在[0,1]上均匀增加,有着明显的Pattern。
假如其出现的顺序是打乱的,就会有两个好处:
- 不会有明显的Pattern
- 57个数完整出现的时候,仍然保证了在[0,1]上是均分的,也就是不会影响其差异性。
这就是Scramble的基本思想,在radical inverse的阶段顺序是打乱的。
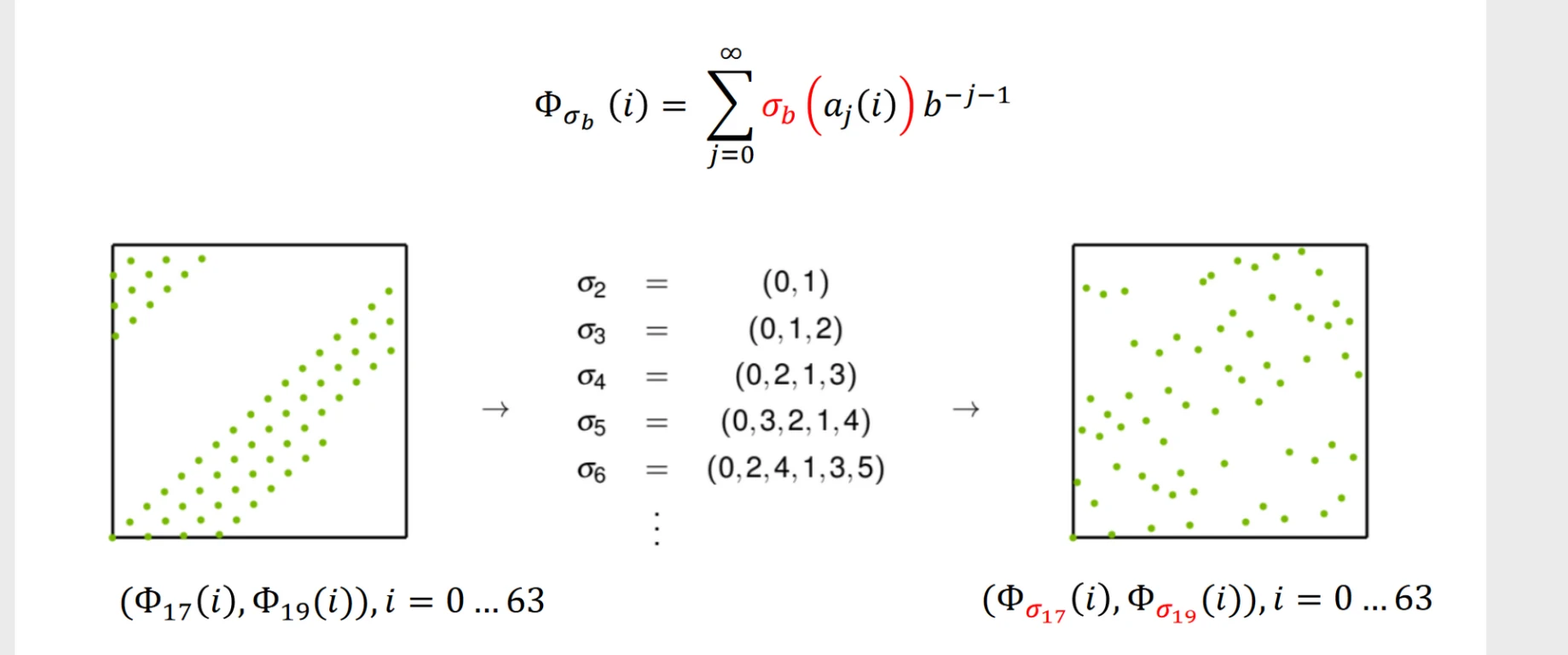
Faure Permutation
一种确定性的打乱方法
以 \(\sigma_5 = \{0,3,2,1,4\}\)为例子
假设我们有一个VDC_5序列
| 十进制数 | 镜像后 | 打乱的采样 | ||
|---|---|---|---|---|
| 0 | 0 * 5^0 | 0 / 5 | sigma_5(0) * 5^0 | 0 / 5 |
| 1 | 1 * 5^0 | 1 / 5 | sigma_5(1) * 5^0 | 3 / 5 |
| 2 | 2 * 5^0 | 2 / 5 | sigma_5(2) * 5^0 | 2 / 5 |
| 3 | 3 * 5^0 | 3 / 5 | sigma_5(3) * 5^0 | 1 / 5 |
| 4 | 4 * 5^0 | 4 / 5 | sigma_5(4) * 5^0 | 4 / 5 |
| 5 | 1 * 5^1 | 1 / 25 | sigma_5(1) * 5^1 | 3 / 25 |
可以注意到,其顺序被打乱了,并且最后产生的序列仍然是这几个数
Faure Permutation的系数打乱顺序是确定性的。
符号 \(\sigma_b\)
- 令 \(\sigma_2 = {0,1}\)
- 当b为偶数的时候,新生成的数组为 \(\{ 2 * \sigma_{b/2}, 2 * \sigma_{b/2} +1 \}\)
有这条规则可以推出,\(\sigma_{4} = \{0,2, 1,3\}\)
- 当b为奇数的时候,复制\(\sigma_{b-1}\),对里面\(\geq \frac{b-1}{2}\)的元素都加1,并且在中间插入\(\frac{b-1}{2}\)
由此可以推出 \(\sigma_3 = \{0, 1, (1+1)\}\)
知道这两条规则就可以直接打表了。


打乱序列0不等于0的情况
朴素算法的实现总是假设第一项恒为0。而Faure Permutation的系数的第0项一般也等于0。假设我们有一个变体的Faure Permutaion,注意起始的行为不同,第0项不等于0。
| sigma_2 | {1,0} |
| sigma_3 | {1,0,2} |
| sigma_4 | {2,0,3,1} |
| sigma_5 | {3,0,2,4,1} |
再用这个序列推算一下VDC_5
| 十进制数 | 镜像后 | 打乱的采样 | ||
|---|---|---|---|---|
| 0 | 0 * 5^0 | 0 / 5 | sigma_5(0) * 5^0 | 3 / 5 |
| 1 | 1 * 5^0 | 1 / 5 | sigma_5(1) * 5^0 | 0 / 5 |
| 2 | 2 * 5^0 | 2 / 5 | sigma_5(2) * 5^0 | 2 / 5 |
| 3 | 3 * 5^0 | 3 / 5 | sigma_5(3) * 5^0 | 4 / 5 |
| 4 | 4 * 5^0 | 4 / 5 | sigma_5(4) * 5^0 | 1 / 5 |
| 5 | 0 * 5 ^ 0 + 1 * 5^1 | 1 / 25 | sigma_5(0) * 5^0 + sigma_5(1) * 5^1 | 18 / 25 |
以上计算过程可以朴素实现成下面这个函数
VDC_5_incorrect(uint64_t inverse) {
uint64_t index = 0;
float invBaseN = 1;
while(Inverse)
uint64_t digit = inverse % 5;
inverse /= 5;
invBaseN *= (1/5);
index = index * 5 + Sigma_5(digit);
}
return index * invBaseN;
}
以\(\sigma_5 = \{0,3,2,1,4\}\)作为例子, 比如
VDC_5_incorrect(0) = 0
VDC_5_incorrect(1) = 3 / 5
但是如果我们代入sigma_5 | {3,0,2,4,1},就会发现VDC_5_incorrect无法正确得到VDC_5_incorrect(0)的值,因为它的内层while被直接跳过了。

PBRT专门处理了这个情况,该写了一下函数
VDC_5_correct(uint64_t inverse) {
uint64_t index = 0;
float invBaseN = 1;
float invBase = 1 / 5;
while(Inverse)
uint64_t next = inverse / 5;
uint64_t digit = inverse % 5;
invBaseN *= (1/5);
index = index * 5 + Sigma_5(digit);
Inverse = next;
}
return invBaseN * (index + invBase * perm[0] / (1 - invBase));
}
当 sigma_{5} = {3,0,2,4,1}:
VDC_5_correct(0) = 3 / 4 = 15 / 20
VDC_5_correct(1) = (3/4 + sigma(1)) /5 = 3 / 20
VDC_5_correct(2) = (3/4 + sigma(2)) /5 = 11 / 20
VDC_5_correct(3) = (3/4 + sigma(3)) /5 = 19 / 20
VDC_5_correct(4) = (3/4 + sigma(4)) /5 = 7 / 20
PBRT的做法相当于额外给了一个常量的偏移(把perm[0]的值给考虑进去了),直接给一个常量偏移不会影响VDC的差异性。 因为差异性实质上是靠点在值域上等间距分布保持的,给一个常量偏移不会破坏这个假设。
随机Shuffle
另外一种Permutation就是随机Shuffle,唯一的问题就是确定性不好。
https://github.com/lgruen/halton/blob/main/halton_sampler.h
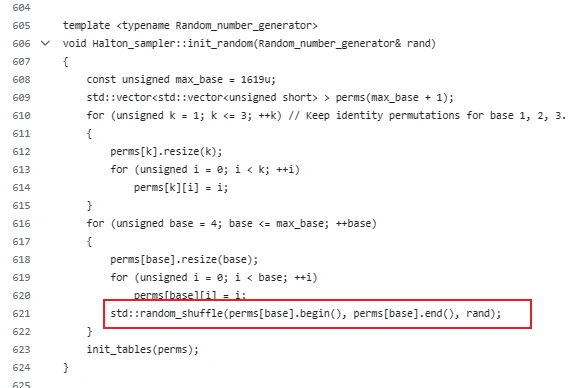
打表法
halton/halton_sampler.h at main · lgruen/halton
- 由于在确定底数的情况下,每个数字的radical inverse都是确定的
- 再加上faure permutation也是确定性的
加起来就可以打表。
比如下面的代码,对于VDC_5进行了一次打表,最大支持到5^3 = 125。
随便取一个数:
| 十进制数 | 5进制的表示 | 镜像后 | 打乱的采样 | |
|---|---|---|---|---|
| 17 | 2 * 5^0 + 3 * 5^1 + 0 * 5^2 (032) | 230 | sigma_5(0) * 5^0 + sigma_5(3) * 5 + sigma_5(2) * 5^2 = 55 | 查表可得55 |
| 123 | 3 * 5^0 + 4 * 5^1 + 4 * 5^2 (032) | 344 | sigma_5(4) * 5^0 + sigma_5(4) * 5 + sigma_5(3) * 5^2 = 49 | 查表可得49 |
表里记录的是反转后的值,没有除以InvBaseN来归一到(0.xxx)。
另外一个推论是如果我们要支持大数,比如114514,我们只需要把他拆分成 \( (14 * 125^0 + 41 * 125 + 7 * 125^2)\),得到 \((14,41,7)\),反转后得到\((7,41,14)\),依次查表,并且重新归一化到(0.)。 归一化系数应该是 \((1 / 125^3)\)。
这里从这个计算过程可以看出,radical inverse可以分组计算,可以1位1位反转,也可以多位一起反转。多位(n)反转的时候,其底数等于\(b^n\)。
// Faure Scrambling以5为底数的permutation为[0,3,2,1,4]
// 下面长度为5^3数组一次可以完成三个数字的permute
static const unsigned short FaurePermutation[5*5*5] = { 0, 75, 50, 25, 100, 15, 90, 65, 40, 115, 10, 85, 60, 35, 110, 5, 80, 55,
30, 105, 20, 95, 70, 45, 120, 3, 78, 53, 28, 103, 18, 93, 68, 43, 118, 13, 88, 63, 38, 113, 8, 83, 58, 33, 108,
23, 98, 73, 48, 123, 2, 77, 52, 27, 102, 17, 92, 67, 42, 117, 12, 87, 62, 37, 112, 7, 82, 57, 32, 107, 22, 97,
72, 47, 122, 1, 76, 51, 26, 101, 16, 91, 66, 41, 116, 11, 86, 61, 36, 111, 6, 81, 56, 31, 106, 21, 96, 71, 46,
121, 4, 79, 54, 29, 104, 19, 94, 69, 44, 119, 14, 89, 64, 39, 114, 9, 84, 59, 34, 109, 24, 99, 74, 49, 124 };
// 注意这个函数最大只能支持到 5^12 = 244,140,625,远小于uint32的值域
// 要满足超过uint32的值域(4,294,967,295)还要再查一次表,需要到5^15
double Halton5(const unsigned Index)
{
// 依次提取0-2,3-5,6-8,9-11位的digits左右翻转并移到小数点右边
return (FaurePermutation[Index % 125u] * 1953125u + FaurePermutation[(Index / 125u) % 125u] * 15625u +
FaurePermutation[(Index / 15625u) % 125u] * 125u +
FaurePermutation[(Index / 1953125u) % 125u]) * (0x1.fffffep-1 / 244140625u);
}