Veach在其博士论文里详细阐述了MIS的理论Multiple Importance Sampling，并给出了一段简单的无偏性证明，但是其过于精简导致我一直没看懂无偏性的证明这一块，尤其是其无偏性的证明需要\(\sum_i\omega_i = 1\)这个条件，花了点时间想清楚。

多重重要性采样

Airguanz同学给出了渲染方程中应用MIS的无偏性证明,不过其符号比较复杂，花了点时间才看懂，因此自己写个笔记吧，也从自己的思路里出发。

\(f(x)g(x)\)函数的估计

从PBRT中取一小节内容作为例子。

假设两个已知形式函数\(f(x)\)和\(g(x)\)，要求的积分为\(\int f(x)g(x) dx\),已知其重要性采样的pdf为\(p_f(x)\)和\(p_g(x)\)那么对其的多重重要性采样可以写作

\[ F = \frac{1}{n_{f}} \sum_{i=1}^{n_{f}} \frac{f\left(X_{i}\right) g\left(X_{i}\right) w_{f}\left(X_{i}\right)}{p_{f}\left(X_{i}\right)}+\frac{1}{n_{g}} \sum_{j=1}^{n_{g}} \frac{f\left(Y_{j}\right) g\left(Y_{j}\right) w_{g}\left(Y_{j}\right)}{p_{g}\left(Y_{j}\right)} \labeltag{1} \]

假设抽样次数相同\(n_f = n_g = n\),那么\(n\)可以提出来，我们只研究单次的采样

\[ F = \frac{1}{n}\sum_{i=1}^{n}( \frac{f\left(X_{i}\right) g\left(X_{i}\right) w_{f}\left(X_{i}\right)}{p_{f}\left(X_{i}\right)} + \frac{f\left(Y_{j}\right) g\left(Y_{j}\right) w_{g}\left(Y_{j}\right)}{p_{g}\left(Y_{j}\right)}) \labeltag{2} \]

Balance heuristic

一种权重\(\omega_s\)的计算方式可以写作，veach指出\(\beta = 2\) 的时候效果不错，不过也可以记为\(\beta = 1\)，不影响无偏性

\[ w_{s}(x)=\frac{\left(n_{s} p_{s}(x)\right)^{\beta}}{\sum_{i}\left(n_{i} p_{i}(x)\right)^{\beta}} \]

那么上述公式中的第一项可以转写为，

\[ \frac{f(X) g(X) w_{f}(X)}{p_{f}(X)}=\frac{f(X) g(X) n_{f} p_{f}(X)}{p_{f}(X)\left(n_{f} p_{f}(X)+n_{g} p_{g}(X)\right)}=\frac{f(X) g(X) n_{f}}{n_{f} p_{f}(X)+n_{g} p_{g}(X)} \]

其中\(n_f,n_g\)是从分布\(pdf_f(x)\)，\(pdf_g(y)\)中采样次数，由于路径追踪中我们每次只生成一根光线，所以其值可以都令为1。整理为

\[ F= \frac{f(X) g(X)} { p_{f}(X)+ p_{g}(X)} + \frac{f(Y) g(Y)} { p_{f}(Y)+ p_{g}(Y)} \labeltag{3} \]

这样当\(p_f(x)\)的值很小的时候，\(p_g(x)\)可能比较大，避免了大方差的引入。

无偏性证明

对式子\(\eqref{2}\)的多重重要性采样估计\(F\)求期望

\[ E(F) = \frac{1}{n}\sum_1^n (E(\frac{f(X_i) g(X_i)} { p_{f}(X_i)+ p_{g}(X_i)}) + E(\frac{f(Y_i) g(Y_i)} { p_{f}(Y_i)+ p_{g}(Y_i)})) \]

对连续随机变量求数学期望的式子为\(E[F] = \int f(x) p(x) dx \),上面的式子带入下来单独拿出来第一项，其变量x是从分布\(p_f(x)\)中取出来的，因此其积分式子中应该乘以\(p_f(x)\),期望为

\[ E_1 = E(\frac{f(X_i) g(X_i)} { p_{f}(X_i)+ p_{g}(X_i)}) = \int \frac{f(x) g(x)} { p_{f}(x)+ p_{g}(x)} * p_f(x) dx \]

同样后面的可以写作

\[ E_2 = \int \frac{f(y) g(y)} { p_{f}(y)+ p_{g}(y)} * p_g(y) dy \]

两个期望的分子均包含\(f()g()\)，假设函数\(f()\)和\(g()\)在函数定义域外的值为0，则对\(f()g()\)积分的积分区间为两个函数的定义域的交集(因为交集外\(f()g()\)必然有一项为0)

因此则两个期望积分式的积分区间相同，对于任意一个x必然能找到和其相等的y，所以在积分域内其\(x,y\)符号可以互换，因此积分的累加可以写作累加和的积分。

Info

对于任意一个\(x\)必然能找到和其相等的\(y\)这一条是证明的关键，而这一条只有在连续积分形式下才能成立。

也即满足Veach论文中的\(\sum_{i=1}^n\omega_i(x) = 1\)这个条件。

在实际的编程实现中，由于\(X\)和\(Y\)分别是对\(p_f(x)\)和\(p_g(y)\)的重要性采样得来的样本，在离散情况下其权重和\(w_1 + w_2\)不能保证始终加起来为1,这是veach的证明最困扰我的地方。但是由于蒙特卡洛积分本身是无偏估计，因此在求期望时其可以在积分形式和离散形式下互相转换(无偏)，所以转换为连续积分的式子就可以继续证明下去了。

只有满足\(\sum_{i=1}^n\omega_i(x) = 1\)这种条件的mis权重计算方式，下面的式子(用的balance heuristic)才能消元成功。

\[ \begin{aligned} E(F) = \cancel{\frac{1}{n}} \cancel{\sum_1^n} (E_1 + E _2) &= \int \frac{f(x) g(x)} { p_{f}(x)+ p_{g}(x)} * p_f(x) dx + \int \frac{f(y) g(y)} { p_{f}(y)+ p_{g}(y)} * p_g(y) dy \\ &=\int \frac{f(y) g(y)} { \color{red}{\cancel{p_{f}(y)+ p_{g}(y)}}} * \color{red}{\cancel{(p_g(y) + p_f(y))}} \color{black}{dy} \\ &= \int f(y)g(y) dy \end{aligned} \]

由此证明其为无偏估计

渲染方程的无偏估计

回到渲染方程,忽略\(L_e\)项重点关注积分式，我们可以注意到其与上式的\(f()g()\)形式相似，其可以分为对光源\(L_i(p,\omega_i)\)重要性采样和对BRDF的重要性采样

\[ L_o(p,\omega_o) = L_e(p,\omega_o) + \int_{\Omega^+}L_i(p,\omega _i)f_r(p,\omega_i,\omega_o)(n \cdot \omega_i) \text{d}\omega_i \]

借用一张闫老师的Games101的手绘图表示，对光源的重要性采样的积分域只包括光源在半球上的立体角的投影部分，如紫色部分，把该区域命名为\(M\)。渲染方程的积分域为整个半球\(\Omega^+\)，我们分拆为\(\Omega^- = \Omega^+ - M\)和\(M\)两个积分域

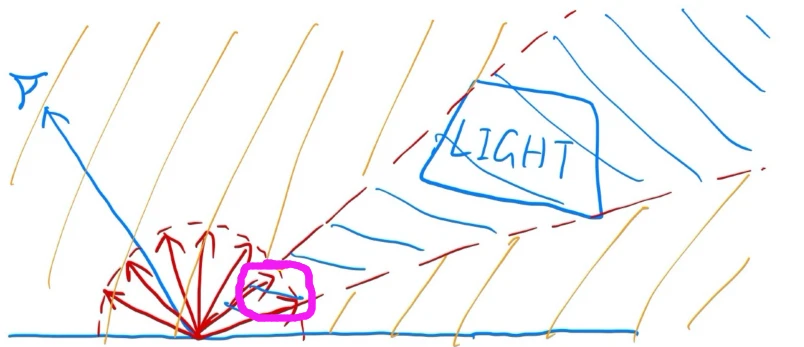
Balance heuristic

\[ L = \int_{\Omega^-}L_i(p,\omega _i)f_r(p,\omega_i,\omega_o)(n \cdot \omega_i) \text{d}\omega_i + \int_{M}L_i(p,\omega _i)f_r(p,\omega_i,\omega_o)(n \cdot \omega_i) \text{d}\omega_i \labeltag{4} \]

注意在光源投影的积分域内，其满足上文所述的\(f()g()\)的形式，已经证明了多重重要性采样的无偏性。

在光源投影外的积分域\(\Omega^-\)，由于对光源的重要性采样所得到的\(pdf\)恒为0(因为该立体角方向在光源投影外，与光源不相交)，带入式子\(\eqref{3}\)，多重重要性采样退化为单纯的BRDF采样，其仍然为无偏估计。

这就是直接光照情况下的多重重要性采样，在直接光照照不到(间接光)的地方其退化为BRDF采样。

NEE(Next Event Emission)

朴素的BSDF采样是每个着色点都沿着BRDF采样出来的下一个弹射方向进行，并且如果在光路弹射过程中没有接触到光源，那么整条光路都浪费掉了。

由此可以衍生出另外一种思想，对于小的光源，直接对光源进行重要性采样可能会得到更友好的采样结果。

化简\(\eqref{2}\)式，代入\(n=1\)

\[ F = \frac{f\left(X_{i}\right) g\left(X_{i}\right) w_{f}\left(X_{i}\right)}{p_{f}\left(X_{i}\right)} + \frac{f\left(Y_{j}\right) g\left(Y_{j}\right) w_{g}\left(Y_{j}\right)}{p_{g}\left(Y_{j}\right)} \]

可以将\(f(X)\)看做BRDF(x),把g(x)看做\(L_i\)。

1.当权重\(\omega_f = 0, \omega_g = 1\)时，此时此公式代表计算都只对光源进行采样(NEE/ShadowRay等名字)。

2.当权重\(\omega_f = 1, \omega_g = 0\)时，此时此公式代表计算都只对BSDF进行采样。

3.当权重\(\omega_f \in [0,1), \omega_g \in [0,1) \)时，此时此公式代表多重重要性采样。

注意NEE在实现中有几个细节需要考虑:

光线第一次弹射需要加上击中点的\(L_e\)，但是后续弹射都不能再加了。因为后续弹射的Radiance都由ShadowRay计算，如果一次弹射同时加上了ShadowRay和命中光源的Radiance，那么一次蒙特卡洛抽样贡献了两个结果，会导致画面偏亮。
碰见(接近)Specular的表面，NEE会失效(因为其BXDF是近似狄拉克函数)，对于这种情况只能回退到BXDF采样。

一个有意思的是不同无偏采样策略的结果加起来还是无偏估计的结果，所以可以写出这样的代码(经单元测试验证通过无偏)，不过对于简单的做平均不能降低噪声水平

for(i = 0; i < spp ;i ++)
{
    use_nee = random() < 0.5;
    radiance = 0;
    if(use_nee)
    {
        radiance += Li_nee(...)
    }
    else
    {
        radiance += Li_bsdf_sampling(...)
    }
}
radiance /= spp; // biasless

NEE实现的伪代码可以见如下, 来源自(https://www.cg.tuwien.ac.at/sites/default/files/course/4411/attachments/08_next%20event%20estimation.pdf)